From wax tablets to elliptical curves. A Brief History of Cryptography (Part Two)

After having broadly reviewed what we could call the genesis of cryptography, in this second article we will take us far forward in time, up to the present day.
With the advent of modern electronic computers, it has been possible to exploit the computational power of processors in order to automate the procedures for coding and decoding messages.
Conceptually, even though centuries have passed, we still think in terms of algorithm, which represents the cryptographic method, and key, a string chosen by the user useful for encrypting and decrypting the message.
A substantial difference with respect to the past is given by the fact that electronic computers use only binary numbers as inputs, i.e., the numbers 0 and 1, with the combination of which all the other numbers, letters and symbols are composed. In particular, for the formation of the alphabet a conversion method called ASCII is used which allows to represent up to 128 alphabetic and symbolic characters through the combination of 7 binary digits.
Furthermore, the introduction of block encryption algorithms has made it possible to speed up the encryption/decryption processes by allowing the algorithm to be applied no longer to single elements, but to entire blocks of elements (composed of N bits), on which it is It is possible to carry out different types of operations, called iterations or rounds which, performed in sequence on each block processed, will lead to a greater or lesser complexity of the encryption algorithm.
Since the 1970s, together with the diffusion of personal computers, there has been great attention to the development of new encryption methods, which guarantee the best compromise between the level of security achieved and the complexity in computational terms of the algorithm adopted. The first of these was created by the German Horst Feistel (German naturalized US cryptographer who worked at IBM on the development of several famous ciphers) who, with his Lucifer cipher , laid the foundations for the Data Encryption Standard (called DES ) first protocol cipher officially adopted by the National Bureau of Standards of the United States ( National Institute of Standards and Technology, an agency of the government of the United States of America that deals with the management of technologies, today NIST ) in order to encrypt documents containing sensitive information ( a brief explanation of DES is available in this NIST document).
After a few years, despite the improvements made over time, the DES protocol was supplanted by the more performing and secure Advanced Encryption Standard (= AES ) which, with its 128-bit blocks, could use 128, 192 or 256-bit keys and which , therefore, has been adopted by NIST to encrypt documents classified even as Top Secret (on this NIST page an excellent presentation of the AES algorithm).
Symmetric encryption and public key encryption
After these very brief references, which I hope to have allowed us to understand how and why we have passed from an analogical to a digital encryption method, it would be appropriate to focus our attention on the functioning of some of them.
Among the encryption methods currently most used in the IT environment, a substantial distinction could be made based on the type of key used: symmetric key encryption and public key encryption.
In the first case, the key to encrypt and the one to decrypt will coincide, in the second case, however, it will be necessary to use two different keys (even if "linked" to each other).
One of the major problems of the first encryption methods, such as DES or AES, just mentioned, consisted in the need to create a rather long key, so as to be reasonably sure that the computational capabilities of the computers could not perform a so-called brute attack force, which is a method that consists of trying all possible combinations of keys. If it is true that it is possible to minimize this risk by simply increasing the length of the encryption key, so as to exponentially increase the calculation times and make a brute-force attack very difficult (if not impossible even with current hardware devices), one must however consider that the main flaw of the symmetric key method was the extreme difficulty in communicating the key to the recipient in a secure way.
This delicate step has been the Achilles' heel of encryption methods of this type for decades, prompting some scholars to look for one that would allow the sender and recipient of the message to communicate in total security.
In fact, there was a piece of history still to be written in cryptography. The moment this dilemma was resolved, a profound revolution would have taken place, in cryptography in particular, but also more generally in the methods of communication believed to be secure until then.
This epochal discovery took place in the 70s in America, developing the intuition had by the mathematicians Hellman, Diffie and Merkle according to which it was possible to exchange unencrypted values useful for generating one's own encryption keys, thanks to the use of functions called unidirectional , i.e. via non-reversible functions.
Shortly afterwards, thanks to the application of other scholars and cryptography enthusiasts such as Rivest, Shamir and Adleman , the cryptography system considered since then among the most important and innovative of this branch of science was developed: the RSA system (here the paper), also known as the public key cryptography system.
The innovative idea consisted in the presence of two different keys, one public, used to encrypt the message, the other private, used to decrypt it. This was made possible thanks to the use of a special one-way function, i.e., a function that was normally very difficult to reverse except under certain conditions (=the use of the private key).
In practice, to use this encryption, each user should have two keys, first of all creating a private key, to be jealously guarded, then deriving a public key from it. This key, as explained by the name itself, is not secret, on the contrary, for the purpose of correct encryption it is necessary to communicate it to the sender of the message, who will use it to encrypt his message thus sending it to the recipient without the worry of having to communicate the key, with the risks that would derive from it. Once the message has been delivered, for example via email, the recipient just has to decrypt the message using his own private key, the only one capable of inverting the special one-way function that underlies this method.
The classic example reported in scientific literature wants Alice and Bob to be willing to exchange a text message. Alice asks Bob for her public key, and Bob sends it to her. Using Bob's public key, Alice can encrypt the message and can proceed to send it. Once Bob has received the message, he can decrypt it using his private key.
In reality, the function used to implement this method is defined as unidirectional, but this does not mean that it is completely irreversible since, through factoring, it is possible to try to go back to the prime numbers used for the implementation of this cryptographic system, even if it is extremely expensive in terms of computational power. To overcome this type of problem, the use of keys that are at least 2048 bits long is now recommended.
On this page you will find an explanation of this algorithm, even with some small illustrations that can facilitate understanding 😊.
For fans of numbers and mathematical problems, I recommend reading the book Fermat's Last Theorem. The adventure of a genius, of a mathematical problem and of the man who solved it (I inserted the link on Amazon for simplicity's sake, but you can find it everywhere, even in any traditional bookstore) once again by Simon Singh, who managed to make a topic in itself difficult exciting, and moreover he succeeded in the huge aim of making me read an enormous amount of figures without me being bored!
Hash functions
Taking up the concept of non-invertible function described above, it will be easier at this point to introduce the concept of hash, since it is based on a one-way function, simple to compute but (hopefully) impossible to invert.
The purpose of this algorithm is to reduce a text (or input) of arbitrary length into a string (called hash value or message digest) of a fixed length.
Moreover, in addition to non-reversibility, therefore the impossibility of going back to the initial message starting from the hash value, this function must respect other important characteristics:
• must produce a string that always has the same length regardless of the size of the input;
• it must allow that, if the hashing function is repeated on the same message, the same output value is always calculated;
• finally, it must ensure that at the slightest change in the input, the algorithm returns a completely different hash value.
The most used hashing protocols are: the MD5 algorithm , one of the first algorithms used for this purpose, very fast and still used to check the integrity of files; the family of SHA algorithms offers an increasing safety factor, the best known are SHA-1 and SHA-256 ; the series of RIPEMD algorithms , the best known of which is the RIPEMD-160, born as a European response to the American MD5 algorithm.
At this address we can have fun calculating the hash value for any portion of text and for files up to 10 MB, using numerous hashing algorithms.
The applications of such a function are many and more widespread than one might imagine. A first example of the use of hashing functions are password databases, where passwords are saved in the form of hash values in order to prevent malicious people who come into possession of them from going back to the real passwords.
Another example would be file integrity checking, where you use the hash value as a checksum to make sure a particular file has not changed.
It is possible to verify the integrity of a message, by comparing the hash value calculated before and after the transmission of the message and verifying that no one has altered the source code since, due to the properties of this function, a minimal variation of the input would cause a complete hash value change. A useful application of this feature is the comparison with pre-compiled hash lists, in order to be able to quickly search for files already registered as viruses or containing malware in general.
Also, in computer forensics the hash function is widely used, in order to preserve the data that is acquired from any type of alteration or manipulation, allowing a rapid integrity check at any time. All data that is duplicated for forensic activities, in fact, assumes validity only if their congruence with the original data is verified.
For those who have never heard of computer forensics, I quote a very comprehensive definition:
“Forensic computer science is the discipline that studies the research, identification, collection, preservation, acquisition, analysis, presentation and evaluation of computer data for evidentiary purposes, in the context of criminal or civil procedural law. The science of computer forensics unfolds in different sectors of technology in order to allow the computer expert to acquire and analyse different types of devices and data.”.
Source: https://www.dalchecco.it/formazione/terminologia/informatica-forense/
Any digital element can be used as an input value for a hash function. A string of text, an image, an audio file, an entire hard disk or any other digital data can "pass" through a specific hash function, returning a digest that will always have the same length, based on the algorithm used.
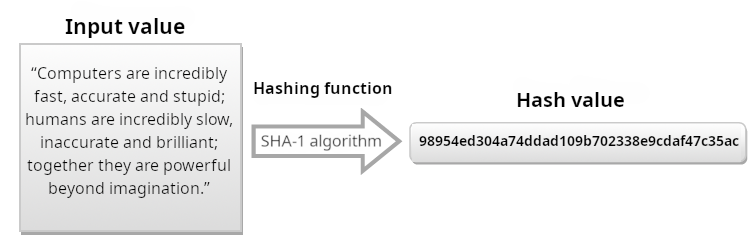
A few brief examples will undoubtedly offer an overview of the above concept, making the characteristics and utility of hash functions immediately identifiable. In particular, for such examples, the SHA-1 algorithm was used:


Note how, as a single character in the input value varies between the two examples above (replacing the final punctuation mark of the example in Fig. 1 with an exclamation mark of the input value in Fig. 2), the result obtained was completely different.
In the same way, it will be easy to observe that, using a much longer text as input, the hash function always returns a value of the same length (the SHA-1 algorithm, taken for example, generates a message digest with a length of 160 bits, represented with 40 characters in hexadecimal value):
Digital signature
A further application of public key cryptography, coupled with the characteristics of the hash algorithm, was the introduction of the so-called digital signature.
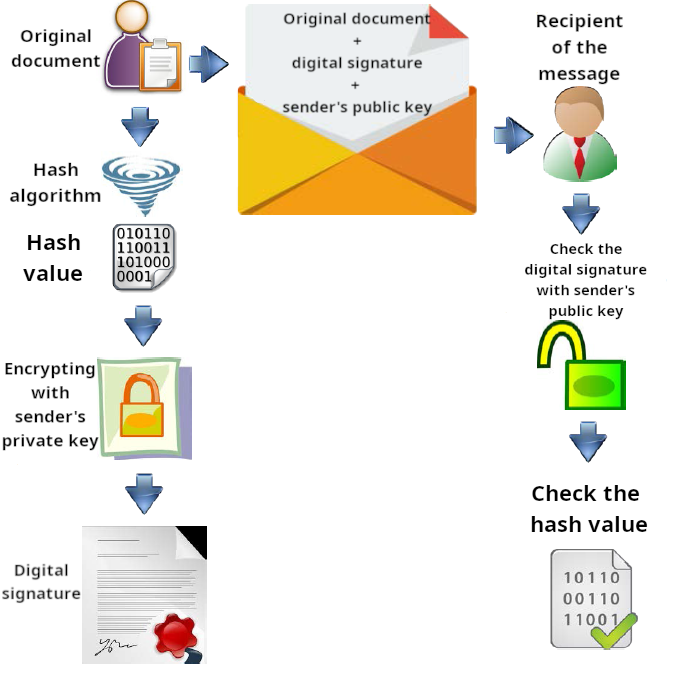
We have already seen that, given a document with content of arbitrary length, it is possible to reduce it to a string using the hash function. This string can be encrypted with the sender's private key, reversing the usual order. At this point, the document is ready to be sent unencrypted to the recipient, together with the digital signature and the sender's public key. The receiver, in turn, using the public key received from the sender, will be able to be certain that the message is authentic and also, by calculating the hash value, that no one has been able to make changes to the original message.
The following diagram will be useful in order to better understand what steps are necessary to apply the Digital Signature to a document:
In recent years, the digital signature has been widely used as well as further implemented, including through the use of smart cards, so as to assume a central role in digital communications, especially in the Public Administration. With D.Lgs. 82/2005, followed by D.Lgs. 235/2010, the Code for Digital Administration was introduced into Italian legislation, a body of rules with which the utmost importance was given to digital communications in the Public Administration, elevating the digital signature to a signature completely similar to the handwritten one (as indicated in article 21, paragraph 2, of Decreto Legislativo 7 marzo 2005, n. 82, published in the “Gazzetta Ufficiale” n. 112 of 16/05/2005).
Also in the Bitcoin protocol the developers have used the digital signature, together with the hash function, to digitally sign the transactions and verify that they originate from the real sender, but we will talk about this in the third and final part.

